SesaBlog

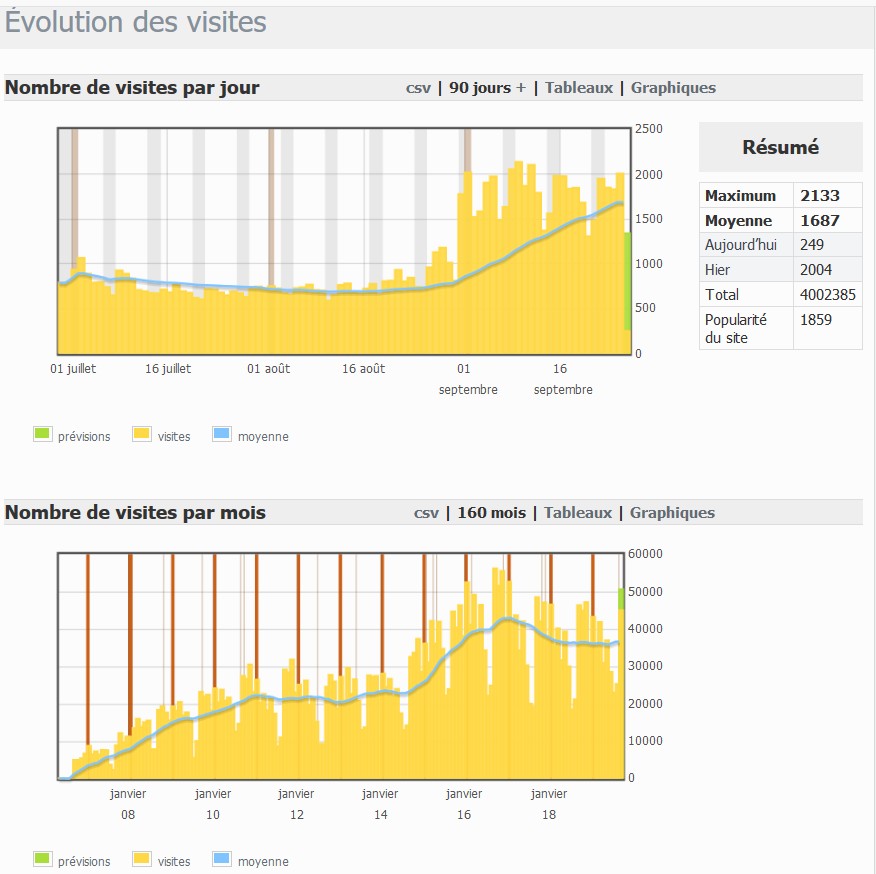
Née en septembre 2006, la revue avait franchi le cap des deux millions de visiteurs en mai 2015 (au bout de 9 ans). En septembre 2019, nous voici au-delà des quatre millions de connexions. L'accélération est sensible, ces chiffres en témoignent (un doublement en quatre ans).

Les statistiques journalières au cours des 90 derniers jours signalent un trafic fourni durant toutes les vacances d'été, qui s'est brutalement accéléré le 31 août.

Les statistiques mensuelles permettent de suivre l'évolution des connexions depuis 2006. La moyenne (courbe bleue) est pour chaque mois celle des 12 mois qui précèdent.

Voici, en date du 26/09/2019, les 30 articles les plus populaires (liste fluctuante d'un jour à l'autre, colonne de gauche) et les 30 les plus visités (liste stable, colonne de droite) depuis leur parution (de 160447 connexions pour le premier à 24086 pour le trentième).

Quelques commentaires (les numéros concernent la colonne de gauche, celle des articles les plus "populaires") :

• L'outil de recherche dans la revue est très sollicité (1).
• Suivent deux articles d'entrée dans les ressources numériques de Sésamath (2, 9).
• On y voit sans surprise les articles liés à l'actualité des nouveaux programmes de 2019 (3, 6, 7 ,12 ,13, 15, 19, 21, 29).
• Trois sites académiques sont fréquemment interrogés (8, 10, 11).
• L'enseignement au Maroc intéresse depuis longtemps les lecteurs (22, 23).
• Les intérêts vont de la Maternelle (30) à l'enseignement Supérieur (25).
• Les jeux (5), l'astronomie (14), les maths en "plein air" (26) et la réflexion philosophique (27)  complètent ce tableau, qui donne une bonne idée des centres d'intérêt variés, entre nouveautés et articles anciens, des lecteurs de MathémaTICE.

Nous remercions chaleureusement les lecteurs pour leur fidélité chaque jour renouvelée. Notre reconnaissance est grande pour les auteurs, dont les propositions d'articles rendent possible la pérennité de la revue.

G.Kuntz

Le numéro 66 de MathémaTICE vient de paraître. 

Les articles du numéro :

• Virginie Gallien présente le site Planète Maths de l’Académie de Grenoble. Dans ce site, les mathématiques prennent des allures de Beaux-Arts ! Elle en montre l’esthétique, la variété et la richesse, elle invite les collègues à en utiliser les ressources dans le travail avec leurs élèves (voir) ;
• René Thomas et le groupe Numatécol de l’IREM de Lyon proposent d’intégrer des robots dans une progression sur la programmation du cycle 1 au cycle 4. L’article s’appuie sur les travaux du groupe de recherche, étalés sur plusieurs années (voir) ;
• Claudine Schwartz invite à une visite guidée d’un site de Bernard Ycart : il y raconte de très nombreuses histoires de mathématiques, illustrées par de magnifiques images et documents. Sous sa conduite, les mathématiques prennent vie et mouvement (voir) ;
• François Goichot s’interroge avec malice : Python sait-il vraiment calculer ? La question se pose à propos de certains sujets d’examens 2019. Tous les langages sont concernés, ainsi que les calculatrices (voir) ;
• Fabrice Houpeaux réfléchit aux rapports entre récursivité en programmation et récurrence en mathématiques (voir) ;
• Benjamin Clerc se penche sur les algorithmes du programme 2019 de Mathématiques, en Première technologique (voir) ;
• Matthieu Brabant s’interroge sur la place des TICE dans les programmes 2019 du lycée professionnel (voir) ;
• Alain Busser revient sur les exemples d’algorithmes de la réforme 2019 du Lycée général, avec leur traduction en Python, qui occuperont bien des collègues durant l’année à venir (voir) ;
• Hédi Abderrahim passe en revue les outils spécifiques qu’offre GeoGebra pour traiter les questions d’arithmétique (voir) ;
• Patrick Raffinat montre pourquoi et comment associer programmation par blocs et programmation textuelle avec Logo, langage très populaire à l’époque du plan « informatique pour tous » dans les années 1980 ; cela le conduit à proposer un logiciel hybride nommé LogoBlocs (voir).

Pour compléter :

• Appel à candidature pour le comité de rédaction de MathémaTICE
• L'appel à contribution 2018-2019
• Toutes les brèves de MathémaTICE
• Vingt-huit parcours thématiques dans MathémaTICE
• Articles à paraître dans les numéros à venir

 Merci d'adresser suggestions, critiques et propositions d'articles à mathematice@sesamath.net

 G. Kuntz

 

L'été permet de trouver un peu de temps long et continu pour acquérir la maîtrise d'outils et de démarches qui amélioreront sensiblement l'enseignement de l'année scolaire suivante. Les quatre parcours thématiques de l'été 2019 à travers MathémaTICE ont cette ambition...

Pour parcourir transversalement MathémaTICE, le moteur de recherche de la revue est un outil de choix. Il opère aussi sur les brèves, qui constituent une des richesses de la revue. Les mots-clés de la page d'accueil facilitent aussi la recherche.

Les parcours des années précédentes restent d'actualité

 

 

La baie de St Pierre et la Montagne Pelée, Martinique (Photo G. Kuntz)

Voici le quatrième parcours 2019.

• Une approche des mathématiques à l’aide d’un logiciel multifonction
• Algorithmique en seconde avec Xcas
• Apprendre des notions mathématiques, géographiques et algorithmiques à l’aide d’un environnement de navigation 3D au-dessus de la Grèce
• Polynômes de Lagrange : récit d’une exploration en Terminale S utilisant les outils informatiques
• MathGraph32 : des figures dynamiques pour appréhender et résoudre des problèmes
• Quelques activités avec R
• Exploration dynamique des infinitésimaux

• Les paradoxes du calcul mental
• Plaidoyer pour l’activité mentale
• Scratch et calcul mental
• Apports du boulier chinois en grande section de maternelle
• Activités mentales et automatismes au Collège et en Seconde : une approche globale
• Refraction : un jeu pour apprendre organisation spatiale, fractions et stratégies...
• Calcul@TICE : Un rallye de calcul mental en ligne à la liaison CM2/6e.

• Programmation en Python pour les mathématiques
• Python et les graphes de fonctions
• À la découverte de Python avec la calculatrice Casio graph90+E
• Séquences d’algorithmique en mathématique en Python 3, de la seconde à la terminale
• De la programmation par blocs à Python, avec SofusPy et PluriAlgo
• Recension de quelques livres sur Python en maths
• Algorithmique et tableur
• La boîte de Pandore des mathématiques expérimentales

 

Dans le cratère de la Montagne Pelée, Martinique (Photo G. Kuntz)

 

Bon parcours dans MathémaTICE !

G. Kuntz

mathematice@sesamath.net

 

L'été permet de trouver un peu de temps long et continu pour acquérir la maîtrise d'outils et de démarches qui amélioreront sensiblement l'enseignement de l'année scolaire suivante. Les quatre parcours thématiques de l'été 2019 à travers MathémaTICE ont cette ambition...

Pour parcourir transversalement MathémaTICE, le moteur de recherche de la revue est un outil de choix. Il opère aussi sur les brèves, qui constituent une des richesses de la revue. Les mots-clés de la page d'accueil facilitent aussi la recherche.

Les parcours des années précédentes restent d'actualité.

 

 

Monastère de La Rábida, Andalousie (Photo G. Kuntz)

Voici le troisième parcours 2019.

1°)  Les articles d'astronomie dans MathémaTICE

2°) De la robotique

• Inirobot et Poppy Education
• Intégrer des robots dans une progression sur la programmation du cycle 1 au cycle 4
• CréaCube, comparaison de la résolution créative de problèmes, chez des enfants et des adultes, par le biais d’une tâche de robotique modulaire
• « Philobotique » à l’Ecole !

• Jeux et TICE, un cheval de Troie idéal pour entrer dans les mathématiques ?
• La course à n contre le chat
• Développer un jeu au collège à l’aide du moteur PACMAN

• L’esprit des probabilités, de l’école au lycée.
• STATISTIX, un site consacré aux statistiques
• Statistiques Médicales En Ligne (SMEL)
• Des probabilités pour la classe dans L@ feuille à problèmes

5°) Divers

• La Tortue Logo : un animal ancien, plein de ressources et d’avenir
• Géotortue : expérimentation en 5ème et pistes à explorer
• Allier mathématiques, algorithmique, programmation avec Scratch
• Mesurer et comparer des périmètres et des aires
• Initiation aux sciences du numérique en seconde
• Apprendre autrement des mathématiques universitaires sur les-mathematiques.net

L'été permet de trouver un peu de temps long et continu pour acquérir la maîtrise d'outils et de démarches qui amélioreront sensiblement l'enseignement de l'année scolaire suivante. Les quatre parcours thématiques de l'été 2019 à travers MathémaTICE ont cette ambition...

Pour parcourir transversalement MathémaTICE, le moteur de recherche de la revue est un outil de choix. Il opère aussi sur les brèves, qui constituent une des richesses de la revue. Les mots-clés de la page d'accueil facilitent aussi la recherche.

• Les exemples d’algorithmes du nouveau lycée général, en Python
• Les algorithmes du programme 2019 de mathématiques de Seconde
• Les algorithmes du programme de spécialité mathématiques de Première (2019).
• Les algorithmes du programme de Mathématiques de Première technologique (2019)
• Les algorithmes du nouveau lycée technologique, en Python
• Quelle place pour les TICE dans les nouveaux programmes en lycée professionnel ?

• Algorithmes et codage au Collège
• Développer un jeu au collège à l’aide du moteur PACMAN
• Débuter la programmation par blocs en 4e
• Algorithmes, programmation : quand le temps s’immisce dans les interfaces
• Programmation événementielle et géométrie dynamique
• Algorithmique : réflexions et ateliers de pratique
• Complément algorithmique pour l’article de Pierre Legrand, "Une curieuse suite récurrente"
• Allier mathématiques, algorithmique, programmation avec Scratch
• Définir des fonctions par un algorithme
• Des sites pour travailler la programmation et l’algorithmique ...
• Programmation et géométrie dynamique
• De l’algorithmique pour faire des mathématiques

3°) Et encore

• Dix ans de ressources mathématiques publiées sur le site de l’académie de Nantes
• Modification et création de ressources dans LaboMep V2
• Le calcul mental, c’est vital !
• Learning apps : des applications pour apprendre
  

• Tout est algorithme, tout est fonction
• De Scratch ou Blockly à Python, en mathématiques
• Les histoires de Bernard Ycart
• Dix ans de ressources mathématiques publiées sur le site de l’académie de Nantes
• Modification et création de ressources dans LaboMep V2
• Le calcul mental, c’est vital !
• Les fractals de Sierpinski
• Un exemple d’usage de calcul@tice en CE1 : transformer les stratégies de calcul
• Autour des usages de la calculatrice en cours de mathématiques au collège
• À la découverte de Python avec la calculatrice Casio graph90+E
• Séquences d’algorithmique en mathématique en Python 3, de la seconde à la terminale

• Les sept chaînes PeerTube de l’IREM de Paris
• Passerelles : enseigner les mathématiques par leur histoire au cycle 3
• Gérard Berry : Où va l'informatique?
• Algorithmes
• Kaninikula, mathématiques aux îles Trobriand
• L’odyssée de pi
• Transhumanisme, entre fascination et illusions

Le numéro 65 de MathémaTICE vient de paraître. 

Les articles du numéro :

• Nathalie Carrié choisit l’approche par une pensée fonctionnelle du programme de Première S. Elle explique comment Snap ! - le Scratch qui code du code - l’a menée à pratiquer la pensée algorithmique en classe.
  Elle aborde alors la totalité du programme de Première S sous cette vision algorithmique. En mettant en avant la notion universelle de fonction, elle transforme avec les élèves tout algorithme en fonction, afin de leur insuffler la graine d’une pensée fonctionnelle pour les aider à mieux appréhender le monde qui les entoure.
  Des exemples éclairants de programmation fonctionnelle fournis en Snap ! et en Python illustrent ses propos (voir) ;
• Benjamin Clerc propose pour les programmes 2019 de mathématiques, en suivant au mieux les préconisations officielles
  • Les scripts en Python pour la classe de Seconde (voir) ;
  • Les algorithmes pour la spécialité de Première (voir) ;
• Patrick Raffinat présente une étude de faisabilité sur l’intégration de ressources algorithmiques (Python ou Blockly) dans LaboMEP ; un prototype est disponible sur le site de développement de J3P (voir) ;
• Hédi Abderrahim aborde les courbes de Bézier en vue d’activités au Lycée, par le truchement de GeoGebra. Ces courbes, nées de l’industrie automobile, ont eu ensuite des champs d’applications élargis. Elles intéresseront à n’en pas douter de nombreux élèves (voir) ;
• Il y a eu longtemps une seule géométrie, euclidienne, qui modélise commodément le monde plat d’une simple feuille de papier. Sont apparues ensuite des géométries non euclidiennes, qui s’affranchissent du cinquième postulat d’Euclide. Ces géométries modélisent un univers différent. Alain Busser et Patrice Debrabant invitent les lecteurs dans le cockpit d’une tortue dynamique pour une exploration d’une de ses plus belles planètes, le disque de Poincaré (voir) ; .
• Pascal Couvrechef se demande si l’approche « créativité » préconisée par les concepteurs de Scratch est compatible avec l’enseignement des mathématiques au Collège ; auparavant, il évoque son importance à l’école primaire (voir) ;
• David Crespil offre aux lecteurs de MathémaTICE un dernier article qu'il consacre au gnomon. Simple bâton planté  à même le sol  pour suivre les ombres du soleil, il donne lieu à des développements mathématiques qui ne  manqueront pas de laisser les lecteurs (et leurs élèves) dans l’admiration ! Le problème des naufragés justifierait à lui seul l’étude de la trigonométrie sphérique… (voir).

Dans ce deuxième article, je vous présente des exercices interactifs à destination des élèves pour s’entraîner que ce soit au niveau première ou terminale sur les suites numériques.

 Des tests ont été effectués sur ces exercices, mais un plus grand nombre de testeurs est nécessaire pour déceler les éventuelles petites coquilles qui pourraient encore se cacher (notamment sur des cas très particuliers). Si vous en trouvez une, n'hésitez pas à contacter l'équipe.

• Suite arithmétique ou géométrique

  Dans tous les exercices cités ci-dessous, chaque question traite aléatoirement d'une suite arithmétique ou géométrique. Il est possible d'imposer un des deux cas à l'aide d'un paramètre, c'est d'ailleurs ce qui est fait dans les exercices classés par chapitres en première.

  • exercice1 où on s'intéresse à la nature d'une suite avec surtout ses éléments caractéristiques

  • exercice2 où on attend le terme général de la suite

  • exercice3 avec la limite d'une suite géométrique

  • Pour ce qui est du calcul de la somme de termes, cela se décline en 3 exercices : pour les suites arithmétiques (exercice4), les suites géométriques (exercice5) et les suites arithmético-géométriques (exercice6).

  Tous ces exercices peuvent être adaptés pour créer un enchaînement permettant l'étude complète de la suite :

  • Nature, terme général et calcul d'un terme particulier pour une suite arithmétique (exercice7) ou géométrique (exercice8).
    Dans ces enchaînements, les données aléatoires sont générées dans la première partie et sont récupérées dans les questions suivantes pour effectuer une véritable étude de la suite. Par exemple :

• Suite arithmético-géométrique

  Les ressources précédentes ont été à la base adaptées pour travailler sur cette famille de suites. C'est pourquoi on retrouvera certaines questions mais elles seront intégrées dans un graphe permettant une étude plus ou moins poussée d'une suite arithmético-géométrique.

  • On peut s'intéresser au terme général de ce type de suite, déterminé à l'aide d'une suite auxiliaire : exercice1.
    
    

  • Cet exercice peut être complété par une question sur la limite du terme général : exercice2.
    
    

  • On peut également demander de manière autonome la somme des termes d'une suite arithmético-géométrique (exercice3), voire une étude plus complète de cette suite avec, pour finir, le calcul de la somme des termes (exercice4). Une aide sur le calcul de la somme peut être apportée (c'est un rappel du cours) en modifiant un paramètre (il faut créer une nouvelle ressource).

  Les liens précédents donnent des exercices où la raison de la suite géométrique intermédiaire est aussi bien positive que négative. Les exercices présents sur Labomep pour le niveau TES sont cependant adaptés pour que la raison soit positive.

• Exercices conduisant l'étude d'une suite arithmético-géométrique

  Deux exercices inspirés de sujets du baccalauréat sont présents pour le niveau ES :

  • exercice1 : où on demande d'exprimer la relation de récurrence vérifiée par la suite à l'aide d'un contexte concret.

  • exercice2 : cet exercice reprend le précédent mais est prolongé par l'étude de la suite arithmético-géométrique.

  L'étude d'une suite arithmético-géométrique peut aussi se retrouver dans un exercice de probabilité en TS comme dans l'exercice3. Par exemple :
  
  
  
  

  
  Dans ces trois exercices, on retrouve un enchaînement de ressources (comme pour les exercices 7 et 8 du paragraphe précédent) où les données aléatoires sont récupérées, ce qui permet l'étude assez complète de la suite telle qu'on en trouve dans les exercices du baccalauréat.

Même si le nombre de ressources sur ce chapitre est assez important, de nouvelles idées sont bienvenues. N'hésitez pas.

L'adresse est "contact arobase sesamath.net" en remplaçant " arobase " par "@".

 --

Rémi DENIAUD.